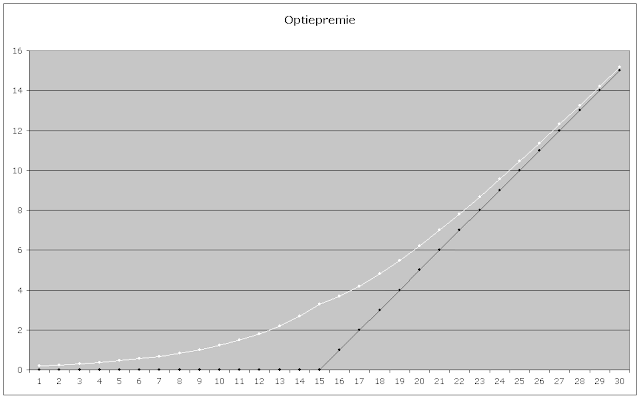
Theoretische waarde

Theoretische waarde

Een optie heeft altijd een bepaald waarde. We betalen bij aankoop van een optie natuurlijk de zogenaamde optiepremie, maar daar zit ook een stuk sentiment in. In een snel stijgende markt is er meer vraag naar callopties. Dat maakt te prijs hoger maar de waarde van de calloptie is en blijft hetzelfde. Die waarde van de optie is de zogenaamde theoretische waarde. 

De theoretische waarde van een optie wordt middels wiskundige modellen berekend, zoals de bekende Black and Scholes formule of het CRR model.  In onze boekenserie over opties wordt uitgebreid behandeld hoe deze theoretische optiewaarde tot stand komt met deze beide modellen.

De theoretische waarde dient als een soort van meetpunt om te zien of een optie duur of juist goedkoop wordt verhandeld. Dus of er teveel premie voor de optie wordt gerekend of gevraagd. Want zoals hierboven al gesteld:   In de praktijk zullen de optiepremie en de theoretische waarde altijd van elkaar afwijken.

De witte lijn in bovenstaande grafiek is de theoretische waarde van een calloptie op een moment ergens in de looptijd. De zwarte lijn is de waarde op de expiratiedag en die is eenvoudig te bepalen. 

Gebruikte begrippen in theoretische waarde

Onderstaande begrippen die in bovenstaande tekst zijn gebruikt zijn elders op deze site gedefinieerd.

optie
  ... met een optie kopen we een recht tot het kopen of verkopen van een onderliggende waarde bijvoorbeeld een aandeel...Lees meer
optiepremie
  ... de optiepremie is de koers van een optie er is een premie voor verkopen en voor het kopen van opties...Lees meer
waarde
  ... de waarde van iets is in het algemeen het geldbedrag dat iets vertegenwoordigt de waarde wordt doorgaans gevonden door de...Lees meer

Begrippen waar theoretische waarde in voorkomt

Onderstaande begrippen zijn elders op deze site gedefinieerd en deze term komt daar in voor.

delta
  ... de deltafactor of delta is de verhouding tussen de premieverandering bij opties ten opzichte van de koersverandering van de onderliggende...Lees meer
wonderaandeel
  ... het u het wonderaandeel al in portefeuille? het wonderaandeel ook wel steraandeel of beurslieveling genoemd is...Lees meer
historische volatility
  ... onder de historische volatility die ook wel de statistische volatility wordt genoemd verstaan we de beweeglijkheid van een fonds...Lees meer
barone adesi model
  ... Het zogenaamde barone adesi model is een uitbreiding op het bekende black &amp scholes optiemodel die het mogelijk...Lees meer
black & scholes
  ... de zogenaamde black &amp scholes formule is een veel gebruikte wiskundige formule waarmee de theoretische waarde van...Lees meer
impliciete rente
  ... de impliciete rente wordt gebruikt bij de berekening van de theoretische waarde van opties ook de impliciete rente moet worden...Lees meer
koersboom
  ... het begrip koersboom komt uit de wereld van het berekenen van de theoretische waarde van een optie...Lees meer
crr binomial model
  ... een bekend wiskundig model om optieprijzen uit te rekenen is het crr binomial model hierbij staat crr voor de...Lees meer
binaire boom
  ... een binaire boom is de basis van het berekenen van optieprijzen volgens het zogenaamde binominaalmodel...Lees meer
kans gewogen opbrengst
  ... als we een bepaalde opbrengst of rendement verwachten is deze niet altijd 100% zeker en dan is er sprake...Lees meer
optiewaarderingsmodellen
  ... in de loop der jaren zijn er vele optiewaarderingsmodellen verschenen om de theoretische waarde van die opties te bepalen...Lees meer
binominaal tree model
  ... het zogenaamde binominaal model of binominaal tree model is een techniek om de theoretische waarde van een optie te...Lees meer
binominaalmodel
  ... het zogenaamde binominaal model of binominaal tree model is een techniek om de theoretische waarde van een optie te...Lees meer
fairvalue
  ... bij warrants en opties is de fair value een andere benaming voor de theoretische waarde...Lees meer
optiemodel van cleeton
  ... het optiemodel van cleeton is net als het model van black and scholes een wiskundige formule om de...Lees meer
cox ross rubinsteinmodel
  ... het cox ross rubinstein model is een binominaal model voor het prijzen van met name amerikaanse opties...Lees meer
cox rubenstein model
  ... het cox rubenstein model is een een wiskundig model om de theoretische waarde van een optie uit te...Lees meer
deltafactor
  ... de deltafactor of delta is de verhouding tussen de premieverandering bij opties ten opzichte van de koersverandering van de onderliggende...Lees meer
coxinger soll ross model
  ... het cox ingersoll ross model is een wiskundig model om opties en dan speciaal in valutaopties te...Lees meer
Fischer Black
  ... fischer black en myron scholes zijn twee amerikaanse financieel deskundigen die voor het eerst een formule...Lees meer
Myron Scholes
  ... fischer black en myron scholes zijn twee amerikaanse financieel deskundigen die voor het eerst een formule...Lees meer
fairtrade
  ... onder een fair trade verstaan we de prijs voor een derivaat die uiteindelijk na verrekening van kosten gelijk is...Lees meer
garman kohlhagen option pricing model
  ... het garman kohlhagen option pricing model is een wat minder bekend statistisch model om de theoretische...Lees meer
non recombining tree
  ... een non recombining tree is een binaire boom waarbij de takken niet bij elkaar komen zoals in onderstaand...Lees meer
fair future price
  ... de zogenaamde fair future price is de theoretische waarde van een future die het onmogelijk maakt om voordeel...Lees meer
theoretische waardebonus of stockdividend
  ... de theoretische waarde bonus ofstockdividend is de koers die als richtsnoer geldt voor de waardebepaling van...Lees meer
claimwaarde
  ... de claimwaarde of de theoretische waarde claim geeft aan wat een claim waard is op basis van de koers van...Lees meer
heath jarrow morton optionpricingmodel
  ... het heath jarrow morton option pricing model is een wat minder gangbaar rekenmodel voor het...Lees meer

Delta benadering

Delta benadering

De delta van een optie wordt meestal als bijproduct (de hedge ratio) uit de Black and Scholes formule berekend, maar er is ook een simpeler vorm van delta benadering mogelijk.

Deze benaderde delta wordt ook wel de empirische delta genoemd.

Delta optie = (slotkoers optie vandaag - slotkoers optie gisteren) / (slotkoers aandeel vandaag - slotkoers aandeel gisteren)

Stel een aandeel gaat van 20 naar 21, en de calloptie gaat van 0.70 naar 0.80 dan is de delta van die calloptie (0.80-0.70)/(21-20) = 0.10/1.00 = 0.10

Het is en blijft een benadering, want we werken bijvoorbeeld met verschillende dagen en verschillende looptijden. De looptijd van gisteren is nu eenmaal een dag langer dan die van vandaag. Ook zal een groot verschil tussen de koersen de volatiliteit beïnvloeden en daarmee de theoretische waarde.

Daarnaast is het aantal metingen veel te klein. Het zou te verbeteren zijn door meerdere opties te nemen en dan een soort gemiddelde uit te rekenen. Dat zou nog een gewogen gemiddelde kunnen worden door bijvoorbeeld de at-the-money waarde zwaarder mee te laten tellen dan een out-of-the-money of deep-in-the-money. Het eindresultaat zou dan iets betrouwbaarder moeten worden. Maar ook dan blijft de steekproef gewoon aan de kleine kant.

Maar met wat beperkingen in de betrouwbaarheid geeft deze delta benadering wel een aardige indicatie.

Gebruikte begrippen in deltabenadering

Onderstaande begrippen die in bovenstaande tekst zijn gebruikt zijn elders op deze site gedefinieerd.

aandeel
  ... In het algemeen gesproken is een aandeel een deel van een gezamenlijke eigendom bijvoorbeeld een aandeel hebben in een nalatenschap...Lees meer
at the money
  ... een at the money optie is een optie waarbij de uitoefenprijs zeer dicht bij de koers van de...Lees meer
calloptie
  ... voor veel beleggers zijn opties het einde ofwel in figuurlijke zin omdat men enthousiast is over de vele mogelijkheden ofwel...Lees meer
delta
  ... de deltafactor of delta is de verhouding tussen de premieverandering bij opties ten opzichte van de koersverandering van de onderliggende...Lees meer
empirische delta
  ... de delta van een optie wordt meestal als bijproduct de hedge ratio uit de black and scholes formule berekend...Lees meer
gemiddelde
  ... het berekenen van het gemiddelde van een reeks getallen is bedoeld om een soort representatief getal voor de gehele reeks...Lees meer
gewogen gemiddelde
  ... we spreken van een gewogen gemiddelde als de afzonderlijke grootheden niet allemaal even zwaar meetellen...Lees meer
in the money
  ... een in the money call is een calloptie waarbij de uitoefenprijs lager is dan de koers van de...Lees meer
indicatie
  ... de indicatie zijn de eerste bied en laatkoersen die een hoekman of de vergelijkbare functionaris die hem op de beurs heeft...Lees meer
laten
  ... onder laten verstaan we het afgeven van koersen waartegen men effecten of valuta wil verkopen ook wordt het gebruikt als...Lees meer
looptijd
  ... het begrip looptijd komen we in de financiële wereld veelvuldig tegen 1 de resterende duur van een obligatielening 2 de resterende tijd...Lees meer
optie
  ... met een optie kopen we een recht tot het kopen of verkopen van een onderliggende waarde bijvoorbeeld een aandeel...Lees meer
opties
  ... in de periode van 624 tot 543 voor christus leefde er een wijsgeer met de naam thales van milete...Lees meer
ratio
  ... ook een ratio is een getalsverhouding tussen twee grootheden kengetallen zijn vaak in de vorm van een ratiokengetallen worden gehanteerd...Lees meer
slotkoers
  ... de slotkoers afgekort tot slot of close is de laatst gedane koers van een aandeel of optie die geldt op...Lees meer
waarde
  ... de waarde van iets is in het algemeen het geldbedrag dat iets vertegenwoordigt de waarde wordt doorgaans gevonden door de...Lees meer

Delta benadering

Delta benadering

De delta van een optie wordt meestal als bijproduct uit de Black and Scholes formule berekend, maar er is ook een simpeler vorm van delta benadering mogelijk.

Delta optie = (slotkoers optie vandaag - slotkoers optie gisteren) / (slotkoers aandeel vandaag - slotkoers aandeel gisteren)

Stel een aandeel gaat van 20 naar 21, en de calloptie gaat van 0.70 naar 0.80 dan is de delta van die calloptie (0.80-0.70)/(21-20) = 0.10/1.00 = 0.10

Het is en blijft een benadering, want we werken bijvoorbeeld met verschillende dagen en verschillende looptijden.

Maar het geeft wel een aardige indicatie.

Delta

Delta

De delta is de mate waarin de premie van een optie verandert bij het veranderen van de koers van de onderliggende waarde. Dat klinkt simpel maar in feite is de delta daarmee één van de belangrijkste kengetallen van de optiehandel.

Bescherming van een aandelenportefeuille met de delta

Zeker als we die handel in opties gebruiken om een aandelenportefeuille te beschermen. Zo geeft de delta ons direct antwoord op een simpele vraag als

.

Hoeveel putopties heb ik nodig om mijn aandelenportefeuille afdoende te beschermen? Toch niet de eerste de beste vraag als we het over een verzekering van die portefeuille hebben. 

Delta is een bijproduct van black and scholes formule

De delta is een bijproduct van de bekende Black and Scholes formule waarmee we de theoretische waarde van een optie kunnen berekenen. In deze Black and Scholes formule wordt deze  delta "de hedgeratio" wordt genoemd.

Omdat we in de aandelenhandel altijd werken met contracten die in het algemeen honderd aandelen bevatten, wordt voor praktische doeleinden de delta met honderd vermenigvuldigd:

Delta = 100 * hedgeratio. 

De delta is bij een calloptie een getal tussen 0 en 1, waarbij het volgende verband bestaat:

putdelta = calldelta - 1 dus een putoptie loopt tussen de -1 en 0

Anders geformuleerd:

put-delta = call-delta -1 

Dit is goed zichtbaar te maken als we de waarden van de put- en de calldelta in een afbeelding zetten, er is altijd een verticaal verschil van 1 tussen de call-curve(bovenste) en de put-curve(onderste).

Zetten we de waarden even in bovenstaande formule dan krijgen we Putdelta = 0,2 - 1 = 0,8

Uit de grafiek blijkt ook de onderlinge verhouding en de extreme waarden. Uit de grafiek blijkt ook de onderlinge verhouding en de extreme waarden. Resumerend:

Verhouding optiepremie en verandering onderliggende waarde

Call options: 0 < Delta < 1

Put options: -1 < Delta < 0

In-the-money opties: Delta nadert de 1 (call: +1, put: -1)

At-the-money opties: Delta is ongeveer 0.5 (call: +0.5, put: -0.5)

Out-of-the-money opties: Delta nadert de 0

Dit geeft ons een goed inzicht in het gedrag dat we van een optie mogen verwachten. De waarschijnlijke verandering van de premie volgt dan direct uit de verandering van de koers van de onderliggende waarde.

Vaak redden we het niet met de delta van één optie. 

Voorbeeld: We hebben een putoptie met een delta van -60. Ons onderliggende aandeel zakt met een euro. Dan zal de optie 60 eurocent meer waard worden. Ofwel, we verzekeren ons aandeel dus niet volledig met deze optie. Daar zouden er minimaal twee (twee contracten normaal gesproken) van nodig zijn en dan zouden we op een daling zelfs nog een kleine winst maken omdat we delta's gewoon bij elkaar op mogen tellen. Twee delta's van 60 zouden dan een delta van 1,20 vormen. En die zou 1,20 euro meer waard worden als de onderliggende waarde een euro daalt.


Voorwaarden goede werking delta
Voorwaarden voor de juiste werking zijn wel dat alle andere variabelen zoals de rente gelijk blijft. Bij de looptijd is dat al lastig want die verandert dagelijks. Maar dan nog krijgen we wel een goede benadering bij niet al te extreme veranderingen.


Bevestiging gevoelsmatig gedrag

De delta maakt een aantal zaken die we gevoelsmatig wel weten, nu meer verantwoord zichtbaar. Bijvoorbeeld: Een deep in the money call optie gaat gewoon met met de koers van het bijbehorende aandeel op en neer. De bijbehorende putoptie doet helemaal niets.

Gebruikte begrippen in delta

Onderstaande begrippen die in bovenstaande tekst zijn gebruikt zijn elders op deze site gedefinieerd.

call
  ... de losse term call kan in diverse betekenissen worden gebruikt in de eerste plaats voor een calloptie en in de tweede...Lees meer
calloptie
  ... voor veel beleggers zijn opties het einde ofwel in figuurlijke zin omdat men enthousiast is over de vele mogelijkheden ofwel...Lees meer
delta
  ... de deltafactor of delta is de verhouding tussen de premieverandering bij opties ten opzichte van de koersverandering van de onderliggende...Lees meer
grafiek
  ... een grafiek is een manier om een reeks getallen zoals koersen visueel weer te geven...Lees meer
hedgeratio
  ... de delta is de mate waarin de premie van een optie verandert bij het veranderen van de koers van de...Lees meer
koers
  ... iedere belegger weet wat een koers is nietwaar hoewel? elder beschrijft in zijn boek een aantal denkbeelden die aardig tot...Lees meer
optie
  ... met een optie kopen we een recht tot het kopen of verkopen van een onderliggende waarde bijvoorbeeld een aandeel...Lees meer
opties
  ... in de periode van 624 tot 543 voor christus leefde er een wijsgeer met de naam thales van milete...Lees meer
premie
  ... de premie van een optie is de koers waartegen deze optie genoteerd...Lees meer
putoptie
  ... een putoptie is een optiecontract dat de houder van de optie koper het recht geeft om de onderliggende waarde op...Lees meer
waarden
  ... met het begrip waarden benoemen we in de effectenwereld waardepapieren in allerlei vormen met name uiteraard effecten...Lees meer